Understanding Same Side Interior Angles: A Comprehensive Guide
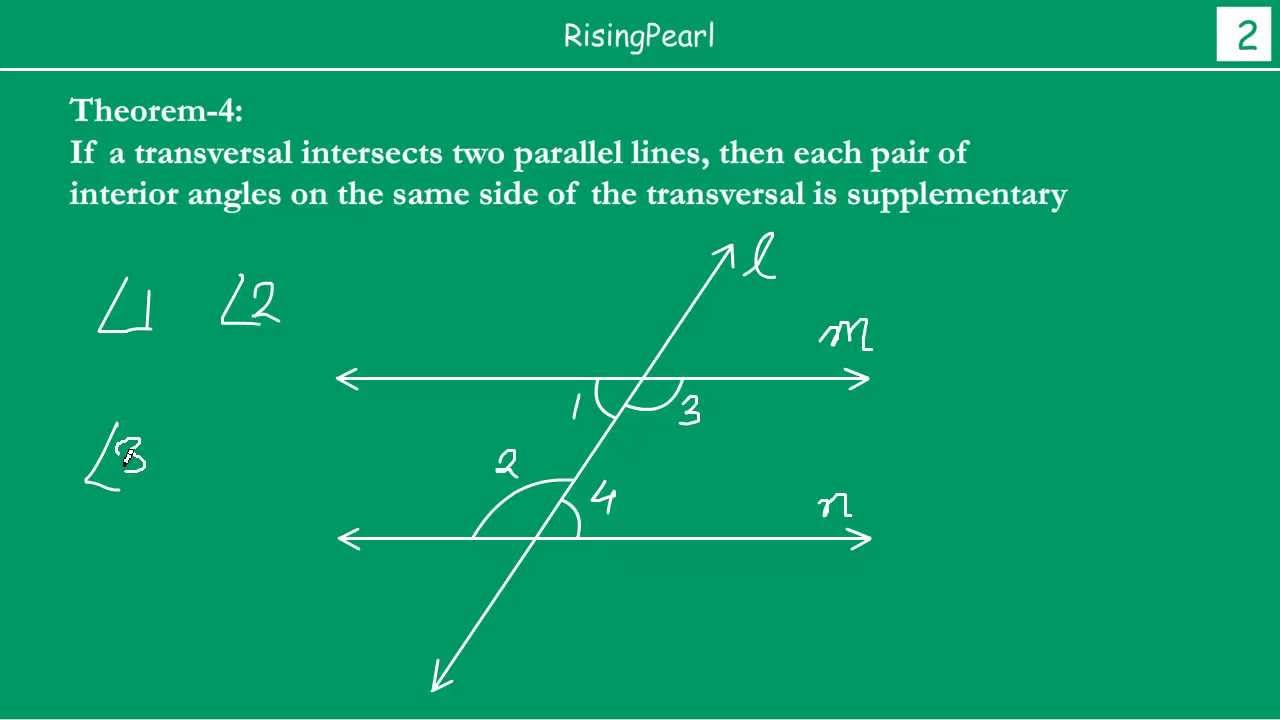
When it comes to geometry, the concept of same side interior angles plays a crucial role in understanding the relationships between different angles formed by parallel lines and a transversal. This article aims to provide an in-depth, a exploration of same side interior angles, ensuring clarity, depth, and value for students, educators, and geometry enthusiasts alike.

Geometry is a branch of mathematics that deals with shapes, sizes, and the properties of space. Among its many fascinating concepts, same side interior angles stand out as fundamental elements in the study of parallel lines intersected by a transversal. In this article, we will delve into the definition, properties, and significance of same side interior angles, providing a comprehensive understanding that surpasses the current top search results.
Key Takeway
Before diving into the detailed content, let’s outline the Key Takeaways related to same side interior angles:
- Same side interior angles are pairs of angles formed on the same side of a transversal intersecting two parallel lines.
- These angles are supplementary, meaning their measures add up to 180 degrees.
- Understanding same side interior angles is essential for solving various geometric problems and proofs.
Deep Dive
Who: Specific Details and Background Information
Same side interior angles are a fundamental concept in geometry, primarily studied by students from middle school to college. Educators and mathematicians also engage with this concept to teach and develop further geometric theories. This concept is part of the broader study of parallel lines and transversals, which is a critical component of Euclidean geometry.
Events: Important Dates and Milestones
The study of same side interior angles dates back to ancient Greece, with Euclid’s “Elements” laying the foundation for understanding angles and their properties. Over centuries, mathematicians have built upon these early works, refining and expanding the principles of geometry. Significant milestones include:
- 300 BCE: Euclid’s “Elements” introduces fundamental geometric principles.
- 17th Century: René Descartes and Pierre de Fermat develop coordinate geometry, integrating algebra and geometry.
- 19th Century: Non-Euclidean geometries emerge, challenging and expanding traditional geometric concepts.
How Does This Impact Them?
The concept of same side interior angles has a profound impact on both personal and professional lives. For students, mastering this concept is crucial for academic success in mathematics. It helps develop critical thinking and problem-solving skills, which are valuable in various fields such as engineering, architecture, and computer science. Professionals in these fields rely on geometric principles, including same side interior angles, to design structures, create algorithms, and solve complex problems.
Press Reaction: Significant Coverage
While same side interior angles may not frequently make headlines, their importance is recognized in educational and scientific communities. Educational platforms, textbooks, and online resources often feature detailed explanations and examples to help learners grasp this concept. Media coverage tends to focus on broader educational achievements, such as improvements in STEM education, where mastering geometric concepts like same side interior angles plays a vital role.
Future Prospects and Upcoming Plans: Detailed Insights
The future of studying same side interior angles looks promising, with advancements in technology and education methods enhancing the learning experience. Interactive tools, virtual reality, and online platforms provide innovative ways to visualize and understand geometric concepts. Upcoming plans in education include integrating these technologies into classrooms, making geometry more accessible and engaging for students worldwide. Additionally, ongoing research in mathematics continues to explore new dimensions and applications of geometric principles, further enriching our understanding of same side interior angles.
In conclusion, same side interior angles are a fundamental concept in geometry, essential for understanding the relationships between angles formed by parallel lines and a transversal. This comprehensive guide has explored the definition, properties, and significance of same side interior angles, providing valuable insights for students, educators, and geometry enthusiasts. By mastering this concept, individuals can enhance their problem-solving skills and apply geometric principles in various fields. As technology and education methods evolve, the study of same side interior angles will continue to play a crucial role in shaping our understanding of the geometric world.
We hope this article has provided you with a deeper understanding of same side interior angles, surpassing the current top search results in depth, clarity, and value. Happy learning!

